Cuántica sin fórmulas – 02/24 La hipótesis de Planck

En la primera entrada de la serie Cuántica sin fórmulas mencionamos los pequeños “flecos” que harían tambalearse a la física clásica hasta que algunas de las cosas evidentes e intuitivas que todo el mundo daba por sentadas demostraron ser totalmente falsas. Hoy vamos a dedicarnos al primero de estos “flecos”, y la semilla de la teoría cuántica, mientras que en la próxima entrada hablaremos del segundo.

Como veremos, ambos son relativamente similares: en ambos casos existe un fenómeno físico del que no tenemos una explicación coherente. En ambos se propone una explicación que se ajustaría perfectamente a la realidad, pero cuyas consecuencias lógicas acerca de cómo es el Universo son tremendas. Y ambos proponentes de estas explicaciones son muy reacios a aceptar esa nueva concepción del Universo, a pesar de ser ellos mismos los que las han planteado.

El primero de ellos, al que está dedicado este artículo, es la radiación de cuerpo negro y la hipótesis de Planck. Dicho mal y pronto, 6,63·10-34 ≠ 0… y el mundo es un lugar muy, muy raro como consecuencia de eso.

A finales del siglo XIX, tanto la termodinámica como el electromagnetismo eran ramas muy sólidas de la física y explicaban excelentemente bien casi todos los fenómenos relacionados con ellas. En algunos de ellos, ambas estaban involucradas a la vez, y uno de ellos era el problema de la radiación de cuerpo negro.

Un cuerpo negro es, como su propio nombre indica, un cuerpo que absorbe absolutamente toda la radiación electromagnética que recibe: ni refleja ni transmite nada de radiación. Un cuerpo de este tipo no es necesariamente de color negro: sí, no refleja nada, pero eso no quiere decir que él no emita radiación. Como absorbe toda la radiación que recibe, si le proporcionamos mucha energía se irá calentando hasta brillar. Puedes pensar en un tizón de madera totalmente negro como un cuerpo negro: si se calienta mucho es una brasa, brilla, no porque refleje luz sino porque emite la suya propia.

Igual que un tizón de madera, según su temperatura, brilla de un color o de otro (rojo profundo si no está demasiado caliente, amarillo si está más caliente, etc.), un cuerpo negro ideal emite radiación con una distribución de frecuencias determinadas. Esta radiación, denominada radiación de cuerpo negro, sigue una curva conocida por los físicos de la época. Dependiendo de la temperatura del cuerpo, la radiación emitida varía, de modo que cuanto más caliente está menor es la longitud de onda en la que tiene un máximo de emisión:

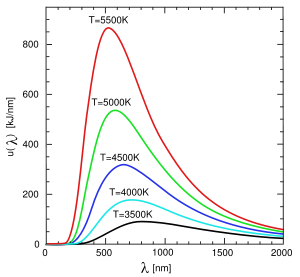
El eje vertical representa la energía emitida en cada nanómetro del espectro electromagnético, y el horizontal la longitud de onda. Como puedes ver, cuanto más caliente está el cuerpo, más radiación emite (lógico), y más hacia la izquierda está el máximo de emisión: un cuerpo bastante frío emite casi toda la energía en la región infrarroja y no lo vemos brillar, un cuerpo más caliente brilla con color rojo, uno muy caliente sería azulado, etc, según la curva tiene un máximo más hacia la izquierda. Una vez más, lógico.

Las teorías de la época suponían que la superficie del material estaba compuesta por una infinidad de osciladores muy pequeños (que hoy diríamos que son los átomos del material) que se encuentran vibrando alrededor de un punto de equilibrio. Cuanto más caliente está el material, más rápido y con mayor amplitud vibran esos minúsculos osciladores, que pueden emitir parte de la energía que tienen en forma de onda electromagnética. Al emitir esta energía, oscilan más despacio: es decir, se enfrían.

Al aplicar estas teorías clásicas a la radiación de cuerpo negro, se obtenía una curva teórica de la radiación emitida…y ninguna curva teórica coincidía con la curva real. La más conocida era la propuesta por Lord Rayleigh en 1900, y perfeccionada por Sir James Jeans en 1905. Era elegante, se deducía de manera lógica a partir de las teorías conocidas… y predecía que un cuerpo negro debería emitir una energía infinita.

La curva que se obtenía a partir de la fórmula de Rayleigh-Jeans se ajustaba muy bien a la curva real para longitudes de onda largas, pero para longitudes de onda cortas divergía de una forma exagerada: no es que fuera algo diferente, es que era totalmente imposible. En descargo de Rayleigh y Jeans, los dos (y también Einstein) se dieron cuenta muy pronto de que la fórmula teórica era imposible.

Esta imposibilidad disgustó mucho a los físicos. De hecho, el fracaso de la ley propuesta por Rayleigh y Jeans suele llamarse “catástrofe ultravioleta” (pues la divergencia se producía para pequeñas longitudes de onda, en la región ultavioleta). Sin embargo, alguien había resuelto el problema sin encontrarse con ninguna “catástrofe” cinco años antes, aunque haciendo una suposición que no gustaba a nadie (ni a su propio creador): el genial físico alemán Max Planck.

A veces se dice, incluso en algunos textos de física, que fue Planck quien se dio cuenta de la “catástrofe ultravioleta” y propuso una fórmula alternativa para resolverla, pero esto no es cierto: Planck había obtenido su fórmula en 1900, cinco años antes de que nadie se diera cuenta de la “catástrofe”. Además, la ley de Rayleigh-Jeans se basa en algunas suposiciones (como el principio de equipartición) con las que Planck no estaba de acuerdo.

Lo que sucedió en 1900, al mismo tiempo que Lord Rayleigh obtenía su propia fórmula e independientemente de él, fue lo siguiente: Planck era consciente de que ninguna de las teorías del momento producía una curva de emisión que coincidiera con la real. Sin embargo, haciendo simplemente una pequeña, una minúscula suposición, y realizando los cálculos de nuevo, se obtenía una fórmula que se ajustaba milimétricamente a la realidad. Una fórmula de una precisión enorme, que explicaba todos los experimentos realizados con cuerpos negros.

Esa suposición era simplemente una pequeña argucia matemática, a la que Planck, en principio, no dio mucha importancia, ni consideró como una concepción del Universo físico. La suposición era que los minúsculos osciladores que componían la materia no podían tener cualquier energía arbitraria, sino sólo valores discretos entre los cuáles no era posible ningún valor.

Dicho de otra manera, lo que todo el mundo (incluyendo al propio Planck) consideraba lógico e intuitivo es que un oscilador puede oscilar como le dé la gana. Por ejemplo, si haces oscilar un péndulo, puedes darle un golpe pequeño (poca energía) o uno grande (mucha energía), de modo que oscile poco o mucho: entre cualquier par de péndulos idénticos que oscilan puedes imaginar otro que oscila con más energía que el primero y menos que el segundo. A continuación puedes fijarte en el primero y el que acabas de inventar: entre ellos puedes imaginar otro que oscile con un poco más de energía que el primero y menos que el segundo, etc.

Sin embargo, si Planck suponía que esto no era así, es decir, que un péndulo no puede oscilar con la energía que le dé la gana, sino que es posible tener dos péndulos oscilando con dos energías y que sea imposible que exista ningún péndulo con una energía intermedia, entonces todos los cálculos que realizaba concordaban a la perfección con la realidad.

De modo que Planck publicó sus cálculos y su suposición en 1901, y durante cuatro años nadie le prestó mucha atención. Aunque no vamos a entrar en fórmulas, Planck supuso que los pequeños osciladores de la materia podían oscilar sólo con energías que fueran múltiplos enteros de una “energía fundamental” que era proporcional a la frecuencia con la que oscilaban mediante una constante que probablemente era muy pequeña.

Pero piensa en lo que significa la hipótesis de Planck: si tienes un péndulo oscilando y le vas dando energía, no la adquiere de forma continua, como si subiera una pendiente poco a poco. Es como si la energía que puede tener fuera una escalera, y tú puedes hacer que suba un escalón de la escalera, o dos, o tres… pero no que se quede entre dos escalones. De ahí que la posterior teoría cuántica, de la que la hipótesis de Planck es el germen, se llame así: la hipótesis de Planck es que la energía de cualquier oscilador está cuantizada, es decir, no tiene valores continuos sino discretos: “escalones” de energía, que hoy llamamos cuantos de energía.

Desde luego, algo parecido había ocurrido antes en física al estudiar la materia: algunos pensaban que la materia era continua, y que un trozo de madera podía ser roto en dos trozos iguales, éstos en dos trozos iguales, y así ad infinitum. Otros pensaban que la materia estaba compuesta de trozos discretos, y que no era posible coger una cantidad arbitraria de materia, sino sólo un múltiplo entero del valor mínimo de materia posible, que no era posible dividir: el átomo. Sin embargo, es relativamente sencillo asimilar que la materia esté cuantizada. Imaginar la energía como cuantizada es mucho más difícil.

En cualquier caso, Einstein fue el primero en recordar a los otros físicos, cuando se dieron cuenta de la “catástrofe ultravioleta”, que la hipótesis de Planck había producido una fórmula que no tenía este problema y que, además, predecía con enorme perfección las observaciones realizadas. El problema, por supuesto, era que aceptar la fórmula de Planck suponía aceptar su hipótesis, y las implicaciones físicas eran escalofriantes -incluso para el propio Planck-.

Pero, puesto que es difícil discutir con un modelo que predice la realidad mejor que cualquier otro, la teoría de Planck fue aceptada, y Max Planck obtuvo el Premio Nobel de 1918, según la Academia “en reconocimiento de los servicios que rindió al avance de la Física por su descubrimiento de los cuantos de energía”. Desde luego, Planck no utilizó la palabra “cuanto” al proponer su teoría, y le costaría años reconciliarse con las implicaciones de su hipótesis, que fue sin duda su mayor logro. La cuántica es así de irónica, e historias similares se repetirían más adelante.

Hoy en día nadie duda de que la hipótesis de Planck es cierta, pero ¿por qué diablos no la notamos? Cuando yo empujo un columpio, o veo vibrar una cuerda, o un péndulo oscilar, no veo que haya valores de energía discretos entre los que hay “huecos”. No veo cuantos, no veo escalones, veo un continuo de energía. La razón es que son escalones minúsculos. Tampoco veo átomos por la misma razón, pero ahí están.

Para que te hagas una idea, si tengo un péndulo oscilando una vez por segundo, y el péndulo tiene una energía de 2 Julios, el siguiente escalón por encima de 2 Julios está en 2,0000000000000000000000000000000007 Julios. No hay ningún valor posible de energía entre esos dos valores. ¡Por supuesto que no veo el escalón! Cualquier tipo de energía que yo le pueda dar al péndulo va a ser muchísimo más grande que ese valor tan pequeño, de modo que nunca podría darme cuenta, en mi mundo cotidiano, de que no es posible que tenga una energía intermedia.

Pero, querido lector, ten en cuenta esto: 0,0000000000000000000000000000000007 Julios no es 0 Julios. Y esa pequeña diferencia, como veremos a lo largo de esta serie, hace que el Universo sea absoluta, totalmente diferente a lo que nuestra intuición nos dice que deberían ser las cosas. El principio de incertidumbre de Heisenberg, la dualidad onda-corpúsculo, el hecho de que los agujeros negros “se evaporen”… todo empieza en esta hipótesis aparentemente inofensiva.

En su hipótesis, como hemos dicho, Planck supuso que el tamaño de estos “escalones” era proporcional a una constante (que fue calculada más tarde, como veremos en el próximo artículo de la serie), la constante de Planck, que hoy sabemos que tiene un valor de 6,63·10-34 J·s. Toda la teoría cuántica, y la diferencia entre el Universo “intuitivo” y el “cuántico”, se basan en ese hecho:

6,63·10-34 ≠ 0.

Bienvenido al mundo cuántico.

En la próxima entrada de la serie hablaremos del segundo escalón (nunca mejor dicho) en el ascenso hacia una teoría cuántica coherente y la destrucción de la realidad objetiva: la extensión por parte de Albert Einstein de la hipótesis de Planck para explicar otro fenómeno que no tenía explicación clásica, y el nacimiento del fotón. Nos dedicaremos al efecto fotoeléctrico.

_________
Tomado de: Pedro Gómez-Esteban González. (2009). El Tamiz. Recuperado de: https://eltamiz.com/el-sistema-solar/