¿Qué es un holograma? [II – Visualización]

La semana pasada hablamos acerca de la creación de un holograma, empleando la interferencia entre un haz de iluminación y otro de referencia. Hoy continuaremos con la segunda parte de aquel artículo: nos centraremos en la visualización del holograma que fabricamos juntos en la primera parte, y hablaremos además de por qué los hologramas se ven como se ven, qué otros tipos hay además del que describimos entonces y en qué se diferencian de casi cualquier otro sistema de almacenamiento de imágenes que pretenda dar impresión de profundidad.

Puesto que aquí hablaremos de cómo ver un holograma y por qué es especial, y una de las razones es la sensación de profundidad, te recomiendo que, antes o después de leer esta segunda parte, leas el artículo de J en El Cedazo acerca de cómo funcionan las televisiones en 3D, ya que explica de manera meridiana la visión estereoscópica y la paralaje y ambos son conceptos básicos para comprender por qué la visión de un holograma “pata negra” es inolvidable.

Como recordarás, lo que habíamos obtenido al final del proceso de la primera parte del artículo era una cosa así:

Es decir, un batiburrillo que no es más que el patrón de interferencia entre los dos haces que incidían sobre nuestra lámina. Las zonas que más luz hayan recibido habrán cambiado más de color, y las que menos –por interferencia destructiva– habrán cambiado menos; y, aunque no lo hayamos dicho hasta ahora, tratamos la lámina de modo que ya no pueda sufrir más cambios químicos, porque si no, no podríamos siquiera sacarla del cuarto oscuro en el que hemos hecho el holograma. En cualquier caso, el resultado está compuesto, si hemos empleado la luz que debíamos –coherente y monocromática– y el material que debíamos –capaz de cambiar su composición a una escala muy pequeña, de modo que tenga gran “resolución”–, por estructuras de un tamaño minúsculo. Y esto es muy importante.

Para entender por qué es importante, y qué hacemos para ver un holograma, debemos hablar antes muy brevemente del segundo fenómeno ondulatorio involucrado en la holografía. Del primero –la interferencia–hablamos en la primera parte del artículo basándonos en otros anteriores. Del segundo no creo haber hablado antes en El Tamiz, y desgraciadamente aún no tenemos ningún bloque de óptica o mecánica ondulatoria publicado, con lo que vamos a hacerlo directamente aquí de una manera cualitativa y lo más simple posible.

Cuando una onda se transmite por el espacio –da igual que sea luz, cualquier otra radiación electromagnética, sonido, olas por el mar, lo que sea– lo hace “punto a punto”. Es decir, según la onda avanza, la energía se va transmitiendo de un punto a otros cercanos a él, éstos se la pasan a otros cercanos a ellos, etcétera. Por ejemplo, si tiras una piedra en un estanque, inicialmente la energía está concentrada en un punto –donde cae la piedra–. El agua en ese punto baja y sube, y los puntos que rodean al punto inicial (si te ayuda, piensa en las “gotas” de agua que rodean el punto donde cayó la piedra) reciben esa energía.

Esos puntos bajan y suben, y cada uno transmite parte de la energía a los siguientes, que se la pasan a los siguientes, etc. Es como si cada punto por el que va pasando la onda se convirtiese en el foco de una “mini-onda”, una fracción minúscula de la energía inicial, que reciben los puntos siguientes; por si quieres leer más sobre este hecho, se conoce como principio de Huygens.

Cuando miras la onda completa (como la ola que avanza por el agua en forma de anillo alrededor de donde cayó la piedra), no ves estas “mini-ondas”, claro, porque se producen todas a la vez. Lo que percibes es la interferencia entre ellas, que no es otra cosa que la onda grande que avanza por el agua, o por donde sea. Para poder ver estas “mini-ondas” que forman, todas juntas, la onda original, te haría falta eliminar partes de la onda para evitar que todo acabe en una mezcolanza de “onda completa”. Pero ¿cómo haces eso?

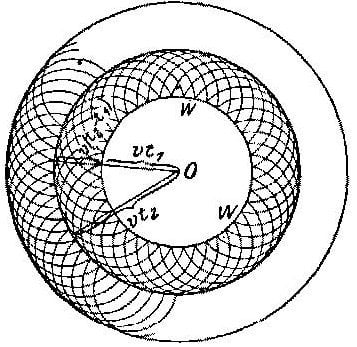
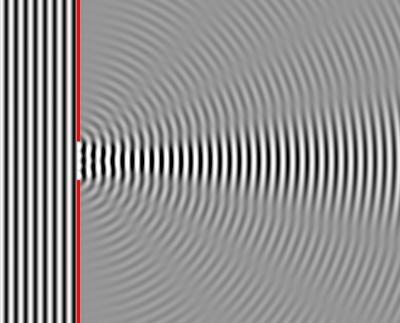
Una manera de hacerlo es, por ejemplo, tapar el camino de toda la onda excepto sólo un trocito pequeño: de esa manera, de todas las mini-ondas que formaban la grande sólo dejas pasar una, y como no tiene ninguna otra con la que interferir, la ves “tal cual es”. Para ello hace falta, por tanto, bloquear el paso de casi toda la onda de alguna manera; en el caso de nuestra piedra, podríamos poner una pared en el agua que pare las olas, pero dejando un agujero en la pared para que pueda pasar una mini-onda y así verla tal cual, sin que interfiera con otras.

Seguro que has percibido algo así en el caso de las olas del mar, cuando se encuentran con un muro, por ejemplo, que tiene una abertura no demasiado grande; en ese caso, de la abertura salen ondas que ya no son “planas”, sino que se parecen mucho más a las de nuestra piedra, es decir, son más parecidas a las ondas que emite una fuente puntual – estás viendo una fracción suficientemente pequeña de las mini-ondas para que puedas notar que están ahí. Si la ola del mar viene desde la derecha hacia la izquierda y el muro es rojo, es una cosa así:

Lo mismo pasa –aunque al principio suene raro– si haces exactamente lo contrario: dejas pasar absolutamente toda la onda inicial excepto un trozo pequeñito, idealmente una “mini-onda” no pasa y todo lo demás sí. Podrías pensar que, ya que cada “mini-onda” es muy poca energía, quitar una no cambiaría absolutamente nada al otro lado, pero no es así. Para ello, piensa en la figura de arriba e imagina que hacemos una especie de “negativo” del muro rojo. Ponemos muro donde está el agujero, y quitamos el muro de donde estaba, con lo que por donde antes pasaba la onda ya no pasa y al revés.

Lo que obtienes entonces es el “negativo” de la onda anterior… con lo que detrás del obstáculo (donde estaba antes el agujero) ves el “negativo” de la pequeña ondita de antes, con lo que también se hace visible el hecho de que hay mini-ondas, sólo que donde antes hubiese una cresta ahora habrá un valle y al revés. Pero, mejor que mis pobres explicaciones, es que lo veas en un vídeo hecho con agua y obstáculos y agujeros:

Como digo, el agujero o el obstáculo debe ser suficientemente pequeño para que esto se note. ¿Cómo de pequeño, te preguntas? Pues de un tamaño comparable a la longitud de onda de las ondas que llegan. En el caso del agua, conseguir esto es bastante fácil, porque la longitud de onda de las olas –es decir, la distancia entre una cresta de ola y la siguiente– es muy grande, pero si se trata de una onda muy pequeña, como la luz, la cosa es muy difícil. Para percibir un punto como un emisor de mini-ondas “independientes”, como en las olas de arriba, nos haría falta un agujero o un obstáculo microscópico.

Y ¿qué hemos conseguido al crear aquel patrón de interferencia sobre nuestra lámina? Sí, lo has adivinado: una rejilla de puntos y rayas microscópicos. Lo que tenemos en la mano, dicho de un modo un poco más técnico, es una rejilla de difracción. Al hacer pasar luz de la longitud de onda adecuada por ella, podemos percibir cada punto de la lámina como emisor de “su propia onda”, en vez de ver un batiburrillo de todas juntas como suele suceder.

La importancia de este hecho es tal que tengo que hacer énfasis en ello: al crear un patrón de difracción sobre nuestra lámina, estamos haciendo que cada punto de la lámina –si hacemos que la atraviese luz– se pueda percibir como su propio emisor de “mini-ondas”. Fíjate en que no estamos haciendo una sola abertura o un solo obstáculo, como en el vídeo de arriba: hemos creado millones y millones de ellos, idealmente uno por punto de la lámina. Y ya sólo nos queda un paso bastante simple para volver a ver la escena a través de nuestra “ventana” tal y como era entonces.

Como recordarás, esta estructura capaz de difractar la luz la hemos producido haciendo interferir el haz de referencia (el “ordenado”, no modificado por nada desde que salió del láser) con el haz de iluminación (el “caótico”, modificado al rebotar en la escena holografiada). El haz de iluminación, tal y como incidía sobre la lámina, es justo lo que queremos “recuperar”. Pero, ahora mismo, está inextricablemente mezclado con el de referencia en nuestra lámina, ya que cada punto tiene su correspondiente cambio químico como resultado de la interferencia entre ambos haces. ¿Qué hacemos entonces? Esto merece un párrafo sólo para esa frase, tal es su importancia:

Volvemos a iluminar la lámina con el haz de referencia.

Para comprender por qué esto es la clave de la cuestión, permite que escriba lo que hemos hecho en una especie de “ecuaciones matemáticas de ful” y creo que se encenderá tu bombilla. Primero hemos iluminado la lámina con la interferencia del haz de referencia y el de iluminación. Las zonas que recibían más luz se han oscurecido, y las que recibían menos luz siguen siendo transparentes, con lo que tenemos el “negativo” de la luz que incidía sobre ella. Para representar esto (que la estructura impresa sobre la lámina es oscura donde había luz y al revés) voy a poner un signo negativo al resultado:

– (Referencia + Iluminación) -> Lámina

Ahora iluminamos otra vez la lámina con el haz de referencia. Pero el de iluminación ya no está. De hecho, nunca podría estar igual que antes, porque eso requeriría poner los objetos exactamente en el mismo sitio, con la precisión extrema que mencionamos en la primera parte del artículo, y tal vez ya ni siquiera disponemos de esos objetos… pero es que da igual. Sólo nos hace falta el haz de referencia.

Lo que hacemos, en estas ecuaciones de ful, es:

Referencia + Lámina

¿Qué obtenemos entonces? Redoble de tambores… no tenemos más que recordar que el conjunto de rayas, puntos y demás estructuras impresas sobre la lámina es el negativo de Referencia + Iluminación:

Referencia + Lámina -> Referencia - (Referencia + Iluminación) -> Iluminación

Hemos vuelto a obtener, a la salida de la lámina, el haz de iluminación. Un haz de luz procedente de objetos que ya no están ahí, cual fantasma de Navidades pasadas. ¿Magia? No: interferencia + difracción.

Creo que la importancia de la interferencia está clara: es a través de ella que hemos obtenido el patrón sobre la lámina. Espero que la de la difracción también lo esté: es mediante ella que cada punto de la lámina se convierte en emisor de los rayos del haz de iluminación, tal y como la atravesaban cuando se grabó el holograma. Y eso es lo que hace especial, especialísimo, a un holograma: que cada punto de la lámina emite rayos exactamente iguales que los que la hubieran atravesado con los objetos detrás. Sin difracción habría “mezcolanza de ondas”, pero con difracción tenemos una miríada de minúsculas fuentes de mini-ondas, discernibles por el ojo como fuentes independientes y resultado de la incidencia, sobre ese punto de la lámina, de todos los rayos procedentes del haz de iluminación que lo alcanzaron en su momento.

Por lo tanto, cada punto de nuestra lámina no contiene información de un solo punto de la escena; contiene la escena completa, ya que es la interferencia de todos los rayos procedentes de cada punto de la escena con el rayo del haz de referencia. También pasa lo contrario: cada punto contiene una información diferente de la escena, ya que a cada uno llegaron rayos casi iguales, pero no exactamente, ya que estaba en una posición algo diferente (claro, si son puntos muy cercanos, las imágenes se parecerán mucho, y si están más lejos, menos). En este sentido se parece mucho más a un espejo o una ventana que a una foto: si rompes una foto en dos, cada trozo de la foto tiene la mitad de la imagen original, pero si rompes un espejo en dos y te miras en él, puedes verte entero, y lo mismo si lo vuelves a romper en más pedazos. La relación no es punto a punto, es punto a escena. Desde luego, cada punto recibe rayos distintos de la escena, con lo cual cada pedazo no te dejaría ver lo mismo (si vieras lo mismo en todos, no habría información extra en cada uno, sería una mera copia), sino una perspectiva diferente de la escena desde cada uno.

Y aquí es donde, en mi opinión, un holograma –que tiene otras limitaciones de las que ya hemos hablado, como lo de la luz monocromática– le da cien vueltas a cualquier sistema de producción de imágenes tridimensionales. Si ves una tele 3D por polarización, por ejemplo –y si no sabes de qué hablo, lee el artículo de J que originó éste–, tu cerebro tiene la impresión de profundidad porque cada ojo recibe una imagen distinta. Hay dos imágenes, y el efecto se produce haciendo que llegue una a cada ojo. ¿Qué pasa si mueves la cabeza hacia la derecha de la pantalla? Pues… nada.

Pero en un holograma hay millones de imágenes, no dos. Cada ojo percibe una imagen distinta porque está recibiendo los rayos tal y como hubieran salido de la lámina de haber objetos detrás, es decir, ligeramente distintos para cada ojo porque tus ojos están en sitios distintos, exactamente igual que cuando miras un objeto real con tus dos ojos y percibes profundidad porque cada ojo lo ve desde una posición determinada. Pero si estás mirando un holograma y te inclinas hacia la derecha, la imagen se va moviendo y va rotando exactamente igual que lo haría si fuera un objeto real, algo imposible en una imagen 3D “normal”. Si hay una lupa en el holograma, puedes mover la cabeza hasta mirar a través de la lupa y ver lo que había detrás de ella ampliado, o retirar la cabeza hacia un lado y no leer lo que había detrás.

Lo que ves, claro, es la escena como la verías a través de una ventana del tamaño de la lámina, con la escena en un cuarto oscuro iluminado sólo por luz monocromática de una sola fuente. Es decir, que no puedes poner en tu cuarto un holograma en la pared con el que puedas ver los Alpes en una mañana de mayo como si vivieras en el Tirol. Además, para que el efecto sea espectacular hace falta una “ventana grande”, porque si lo haces con una muy pequeña es como ver la escena por un agujerito en la pared, desde el que no se ve profundidad ni tiene la menor gracia, y hacer un holograma grande no es fácil. Pero, si se hace bien y se reproduce bien, el efecto es indescriptible. Desgraciadamente, la propia naturaleza de la holografía hace que me sea absolutamente imposible enseñarte un holograma “de verdad” a través de la pantalla o el papel, pero te recomiendo que, si vas a algún museo de ciencia, intentes ver algún holograma de transmisión como el que hemos descrito que tenga cierto tamaño, porque merece la pena.

Hay otros tipos de hologramas, como los de reflexión, que son bastante utilizados. En ese caso, en vez de dividir el haz en dos como en el interferómetro de Michelson, se hace incidir el haz sobre el objeto, se refleja en él y luego interfiere de vuelta con el haz inicial, que actúa de referencia. El mecanismo, sin embargo, es básicamente el mismo y el resultado también es impresionante.

Ya sé que estoy pesadito, pero es que es, de verdad, impresionante. El problema es que casi todos los hologramas que vemos son, francamente, una patata comparados con los de “verdad” –en un momento vemos por qué–, con lo que la idea general parece ser que es una cosa nada impresionante cuando, realmente, no es así. Aunque, como digo, no puedo enseñar un holograma de veras, aquí tienes un vídeo en el que se ve un auténtico monstruo hecho en los 80. Al ser un vídeo, puedes ver cómo cuando se mueve la cámara, lo que se ve en la lámina se mueve, exactamente igual que si estuvieras mirando dentro de la habitación por una ventana:

¿Por qué los hologramas que solemos ver no se parecen, ni en pintura, a éstos que muestro aquí (y el efecto es algo que sólo puedes experimentar de veras si los ves en vivo)? Porque el objetivo de los hologramas utilizados comercialmente no es impresionar, ni siquiera mostrar las cualidades especiales del holograma por su valor en sí mismas. Irónicamente, las aplicaciones típicas de los hologramas se aprovechan de lo puñetero que es crearlos para hacer difícil que algo sea copiado.

Claro, falsificar algo valioso sólo tiene sentido si copiarlo cuesta menos del valor real de esa cosa… pero hacer un holograma es muy, muy caro, por el equipo necesario para crearlo. De este modo, si compras el equipo para fabricar algo (aunque cueste mucho dinero al principio), una vez que hayas fabricado un número enorme de copias, el precio por copia se hace admisible mientras que, al mismo tiempo, hace difícil que alguien pueda copiarlo.

Los ejemplos más típicos son los de los hologramas de seguridad en las tarjetas de crédito (como la palomita de Visa) y en los billetes. Pero ¡ay!, ésos no son hologramas “de verdad”. Antes de que pongas el grito en el cielo, deja que me explique: técnicamente sí, se llaman hologramas, y en un momento vemos cómo se hacen. Sin embargo, en mi humilde opinión, yo los llamaría más bien hologramas parciales o pseudo-hologramas, porque no guardan toda la información visual de la imagen, que es lo que venimos repitiendo todo el tiempo durante este artículo bipartito es lo que define realmente a un holograma.

El problema de utilizar un holograma “de verdad” como marca de seguridad es que, como hemos visto, hace falta luz monocromática y coherente para verlo, y eso no es fácil de hacer. Seguro que, en algún momento del artículo, te has preguntado ¿no podría verse al menos algo con luz normal y corriente? Lo mismo se preguntó, a mediados de los 60, Stephen A. Benton, que trabajaba por entonces para Polaroid. La respuesta es que sí: se puede conseguir fabricar un holograma que sea visible con luz blanca y desordenada, pero sólo si se pierde parte de la información visual y, básicamente, toda la paralaje en un eje.

Prácticamente todos los hologramas que se ven en la vida cotidiana son precisamente hologramas de Benton, también llamados de arcoriris, y culpa suya es lo poco impresionados que estamos normalmente por los hologramas, ¡porque los que vemos son de ful! Aunque no voy a explicar en detalle el proceso de fabricación de estos hologramas de Benton de las tarjetas de crédito, sí quiero intentar explicar en qué se diferencian –para lo bueno y lo malo– de los hologramas “pata negra” que hemos visto antes.

Básicamente, la idea de Benton fue tomar primero un holograma normal del objeto. A continuación realizó el proceso otra vez, es decir, tomó un holograma del holograma original, sólo que en este caso interpuso ante la lámina una placa con una finísima rendija horizontal, que produce la difracción de la luz que le llega. Esto significa, desgraciadamente, que toda la información de perspectiva en el eje vertical se pierde en el holograma final, pues hemos “tapado” uno de los dos ejes con la rendija. Pero es que aún no hemos terminado.

Una vez hecho el segundo holograma, hace falta algo más: copiarlo. Porque claro, no vas a hacer todo este tostón, con lo que cuesta, para cada tarjeta de crédito que fabricas. Con lo que después se toma el holograma y se hacen copias sobre otro sustrato, uno por cada tarjeta de crédito. Aunque este proceso es muy preciso, el resultado nunca es exactamente igual que el original y ahí también se pierde algo de calidad de manera inevitable. Finalmente, la copia del holograma del holograma (ya ves que a estas alturas estamos ya bastante alejados del origen del proceso), que es un holograma de transmisión pero no ya “completo”, se pone delante de una lámina metálica que refleje la luz, y está listo para ser visto.

Cuando llega luz blanca al holograma de Benton, lo atraviesa, se refleja sobre el metal que hay detrás y luego vuelve a atravesarlo según sale hacia tu ojo. Pero ahora el patrón de difracción del holograma –que sigue siendo un holograma de transmisión, ya que está iluminado desde detrás– ya no es un patrón debido únicamente a la interferencia del haz de iluminación con el de referencia, ya que se creó con un elemento nuevo: la rendija. El patrón debido a la rendija horizontal hace que la luz de cada color se difracte de manera diferente, con lo que los colores se separan.

El resultado es que, a pesar de estar iluminando el holograma con luz blanca, tú ves luz monocromática, porque sólo ves una parte de la luz que sale del holograma, la del color que se corresponda con el ángulo con el que miras. Si lo miras desde “más arriba” o “más abajo”, el color cambia, de modo que puedes verlo rojizo, verde, amarillo… pero la escena no cambia en absoluto, ya que los rayos de cada color se comportan igual que los demás.

Por eso, si miras la palomita de Visa e inclinas la tarjeta hacia delante o atrás, sigues viendo siempre la misma palomita, sólo que el color cambia. Ahí es donde hemos perdido una gran cantidad de información, a cambio de poder ver la paloma con luz que no es monocromática ni coherente. Para ver la parte holográfica de la palomita tienes que cambiar el ángulo a izquierda o derecha, o moviendo la tarjeta o moviéndote tú: y ahí sí, si te fijas, verás que la palomita “se gira”. El color apenas cambia, porque no estás “subiendo” ni “bajando” por el arcoiris en el que se ha dispersado la luz, sino que estás viendo rayos con ángulos diferentes dependiendo de la posición en la que la miras.

Desde luego, no es impresionante, y mucha gente ni siquiera tiene sensación de profundidad alguna al mirarla… pero es que, claro, el propósito no es ése. Aunque no veas perspectiva ni profundidad, lo que es innegable es que la palomita es “rara”; me refiero a que, si sacas una fotocopia de la tarjeta de crédito, por mucha resolución que tengas, no se va a parecer al original ni en broma, sino que hace falta un equipo muy caro y conocimientos técnicos complejos para hacer la maldita paloma – y ésa es precisamente la razón de que esté ahí.

Por eso me parece curioso el hecho de que durante cierto tiempo nos costó hacer hologramas por lo difícil que es hacerlos, pero al final –salvo que alguien lo remedie, esperemos que sí– la principal virtud de los hologramas en su aplicación práctica ha resultado ser… ¡el hecho de que son difíciles de hacer! No su belleza, ni la vasta información que contienen, sino la dificultad técnica y económica. En fin.

Mi esperanza es que, según siga avanzando la técnica, podamos ver hologramas más a menudo pero no como marca de seguridad, sino por su propio valor. Hacen falta varias cosas: en primer lugar, conseguir iluminar escenas con luz de varios colores para tener hologramas en color. En segundo lugar, conseguir realizar hologramas sobre un sustrato con tal rapidez que podamos tener “fotogramas holográficos”, y poder así ver una película de este modo.

Aunque hacer predicciones siempre es arriesgado, porque sueles acabar quedando como un pazguato, creo que los hologramas no sustituirán a otros métodos de producir imágenes en 3D como los otros que describe J. Cuando ves una película en 3D, en el cine o en casa, no estás moviéndote de un lado a otro, sino que sueles estar parado: y si lo estás, es muy fácil producir una sensación de profundidad simplemente enviando imágenes diferentes a cada ojo. Es incluso posible permitir que la imagen mostrada cambie según te mueves si tienes algún dispositivo en la cabeza –como gafas– que pueda enviar una señal al ordenador o la TV de modo que ésta simule la holografía, cambiando la dirección de los rayos que te llegan. ¿Quiere esto decir que los hologramas de verdad serán inútiles en el futuro, o seguirán siendo una curiosidad de museo? Creo que no.

En primer lugar, la enorme información almacenada es maravillosa para ciertos usos. Por ejemplo, si pudieras tomar un vídeo holográfico en color de un suceso o escena, quedaría almacenada para la posteridad con una riqueza inmensamente mayor que en un vídeo. Si se trata de algo como una operación quirúrgica o la elaboración de una obra de arte, aprender de ella sería maravilloso porque, si la superficie de grabación es suficientemente grande y cercana a la escena, podrías caminar alrededor y, prácticamente, asomar la cabeza sobre el hombro del artista o cirujano para ver lo que hace como si estuvieras allí.

En segundo lugar, el hecho de que un holograma guarde una inmensa cantidad de información usando la óptica es valioso en sí mismo: cada vez nos hacen falta nuevos medios de almacenamiento de información en los ordenadores, y la memoria holográfica puede ser una alternativa muy interesante en el futuro. Ya hay algunas empresas que han fabricado prototipos de memoria holográfica, aunque creo que quedan años para que algún sistema de este tipo salga al mercado.

_______
Pedro Gómez-Esteban González. (2009). El Tamiz. Recuperado de: https://eltamiz.com/