
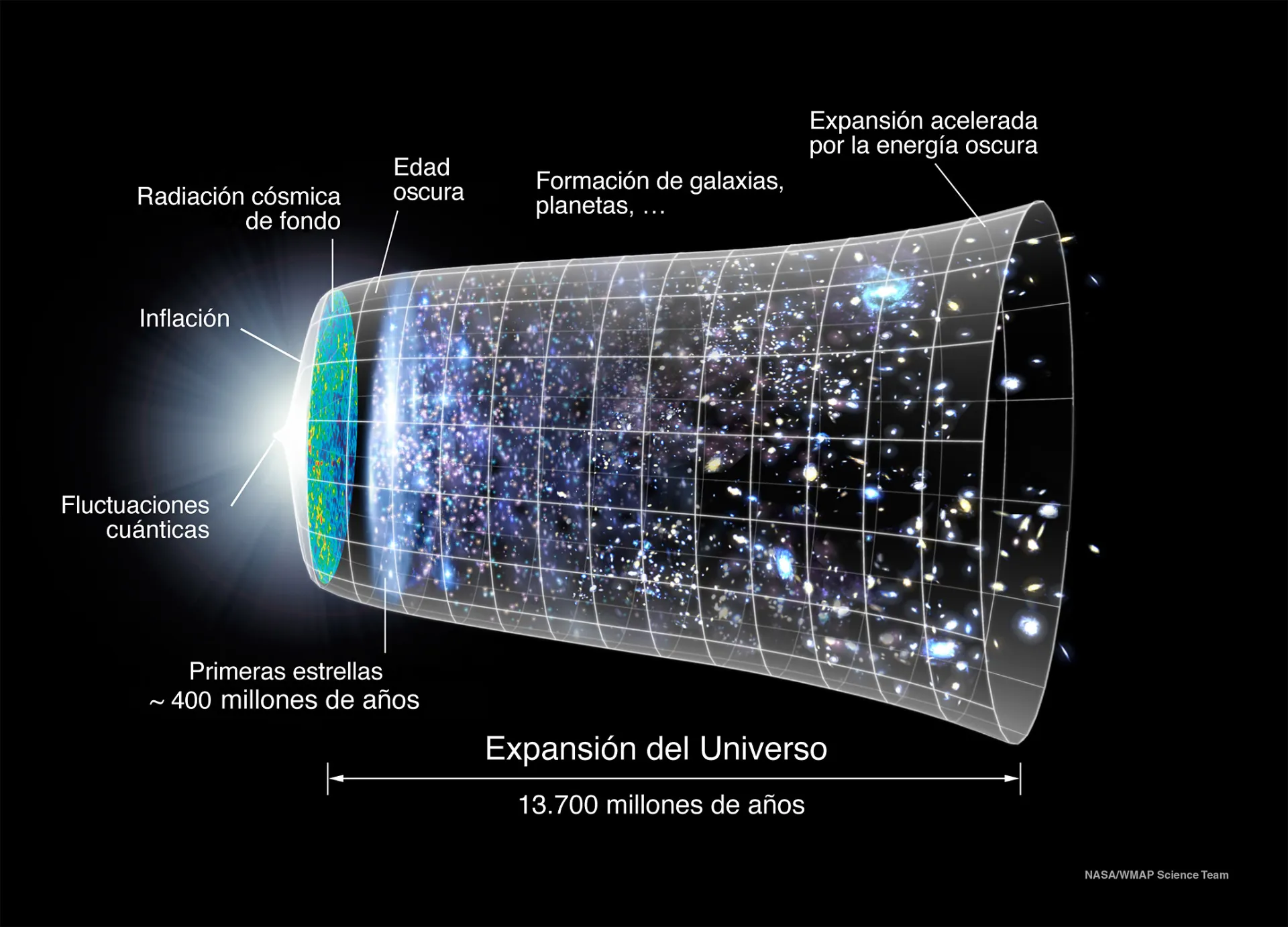
Los modelos de Friedmann-Lemaître-Robertson-Walker (FLRW) son fundamentales en cosmología, ya que proporcionan una descripción matemática precisa del universo a gran escala. Al asumir la homogeneidad e isotropía, estos modelos permiten a los cosmólogos predecir la evolución del universo a partir de unas pocas variables fundamentales, como la curvatura del espacio y la constante cosmológica. Estos modelos son la base para entender conceptos como la expansión del universo, la cosmología del Big Bang, y la influencia de la energía oscura.
En el contexto de los modelos de Friedmann – Lemaitre – Robertson – Walker, cuales valores o rangos de los parámetros k y Λ corresponden a universos con las siguientes características?
a) El universo no es homogéneo ni isotrópico.
(b) No hay posibilidad de una gran explosión.
(c) Un big bang es posible, pero hay al menos otra posibilidad (supongamos que ρ > 0).
(d) El punto particular en el espacio donde ocurrió el Big Bang todavía puede ser determinado mucho después del evento.
(e) En cualquier momento, las propiedades geométricas a gran escala del espacio son idénticas a las de un espacio tridimensional con una geometría plana.
(f) El espacio tiene un volumen finito, y las líneas "rectas" que inicialmente son paralelas eventualmente se encuentran.
(g) Hay una gran explosión, pero el volumen del espacio es infinito desde los primeros tiempos.
Los modelos de Friedmann-Lemaître-Robertson-Walker (FLRW) son soluciones de las ecuaciones de campo de Einstein en la relatividad general que describen un universo homogéneo e isotrópico a grandes escalas. Estos modelos dependen de dos parámetros principales: la curvatura espacial $ k $ y la constante cosmológica $\Lambda $. A continuación, se detalla cómo los valores o rangos de $ k$ y $ \Lambda$ se relacionan con las características específicas del universo mencionadas:
Los modelos FLRW asumen por definición que el universo es homogéneo e isotrópico a grandes escalas. Cualquier descripción de un universo que no sea homogéneo ni isotrópico cae fuera del alcance de los modelos FLRW. Por lo tanto, esta condición contradice las suposiciones fundamentales de los modelos FLRW.
La posibilidad de una "gran explosión" o Big Bang está intrínsecamente ligada a la dinámica del universo descrita por las ecuaciones de FLRW y no se excluye directamente por valores específicos de $ k $ o $ \Lambda $. La idea de que no haya Big Bang podría asociarse más con un universo estático, lo cual requeriría un equilibrio delicado entre $ \Lambda $ y la densidad de materia/energía del universo, pero incluso en la teoría de la relatividad general de Einstein original, se mostró que estos universos son inherentemente inestables.
En los modelos FLRW, un Big Bang es posible para cualquier valor de $k $ y $\Lambda $, siempre y cuando la densidad de energía $ \rho > 0 $. La otra "posibilidad" puede referirse a un universo que se expande indefinidamente o recolapsa en un Big Crunch, dependiendo de los valores relativos de $ \rho $, $ \Lambda $, y $ k $.
Esta declaración es un malentendido común. El modelo de Big Bang sugiere que el Big Bang ocurrió en todas partes al mismo tiempo, no en un punto particular en el espacio. Los modelos FLRW, siendo homogéneos e isotrópicos, no permiten la identificación de un punto único donde ocurrió el Big Bang.
Esto corresponde a un universo con curvatura espacial $ k = 0 $. En los modelos FLRW, $ k = 0 $ describe un universo con geometría espacial plana.
Esto se describe por un universo con curvatura positiva, $ k > 0 $, correspondiente a un universo cerrado en los modelos FLRW. Este universo tiene un volumen finito y la geometría de un espacio esférico.
Un universo que se expande desde un Big Bang con un volumen espacial infinito se describe con $k \leq 0 $. Específicamente, $ k = 0$ para un universo plano o $ k < 0 $ para un universo abierto con curvatura negativa. En ambos casos, el universo puede comenzar con un Big Bang y expandirse a un volumen infinito.
En resumen, los modelos FLRW proporcionan un marco para entender la evolución del universo bajo suposiciones de homogeneidad e isotropía, con la dinámica específica del universo determinada por los valores de $ k $ y $ \Lambda$.
Los modelos FLRW nos han permitido hacer predicciones verificables sobre la estructura y el destino del universo, muchas de las cuales han sido confirmadas por observaciones astronómicas. Su importancia radica en su capacidad para simplificar la complejidad del universo a principios comprensibles y para proporcionar un marco coherente que vincula la teoría de la relatividad general con la cosmología observacional. A través de estos modelos, hemos ganado una comprensión profunda de nuestro universo, desde el Big Bang hasta el presente, y hemos vislumbrado posibles futuros para el cosmos.


