

La semana pasada, en la serie Hablando de… hablamos de la teoría del caos originada en parte a raíz de los trabajos de Poincaré, Lorenz y May. Hoy, si tienes arrestos, vamos a zambullirnos juntos en las turbulentas –ja, ja, ja, qué chispa– aguas del caos en un caso concreto para ver cómo surge poco a poco de donde menos podríamos esperarlo, dentro de la serie Alienígenas matemáticos. El último artículo de esta serie, por cierto, fue sobre fractales, y no por casualidad, como veremos luego.
Afortunadamente para todos, May, Lorenz y Poincaré nunca leerán este artículo. Desafortunadamente para ti, es posible que tú sí lo leas pero, si no conoces esta serie, permite que empiece con un consejo: no lo hagas. Es pedante, absurda y dañina para el sistema nervioso central. Pasea al perro, mira la televisión o medita mientras observas el movimiento de las nubes, ya que cualquier actividad es más útil que la lectura de este artículo.
¿Ya se han ido? Bien, entonces un aviso en serio: vas a leer un artículo denso. Ni siquiera voy a incluir demasiadas tonterías alienígenas. Es difícil ir más allá del típico “el caos se produce cuando un sistema es impredecible por ser muy sensible a los cambios en las condiciones iniciales” sin empezar desde bastante atrás e ir descubriendo cosas poco a poco. Eso es algo que no quiero pedir en la serie Hablando de…, pues mucha gente la disfruta porque es una lectura relajada que no supone gran esfuerzo, pero aquí sí puedo pedirte paciencia y esfuerzo y, de hecho, eso es lo que estoy haciendo ahora mismo.
En este artículo en dos partes te iré pidiendo que utilices un pequeño programa para calcular cosas tú mismo y, ojalá, que llegues a experimentar en primera persona la aparición del caos y algunas de sus propiedades; el caos en sí mismo ni siquiera surgirá hoy, sino en la segunda parte, de manera que paciencia. Hoy me preocupa más asentar ideas como el estado del sistema, las variables que lo definen y la formalización de la evolución de un par de sistemas sencillos.
Antes de empezar con nuestra ridícula y absurda historia de hoy, quiero retomar una idea fundamental que mencioné en el artículo general sobre el caos: el hecho de que un sistema sea muy sensible a las condiciones iniciales no lo convierte en caótico. Se trata de una condición necesaria (es decir, todo sistema caótico es muy sensible a las condiciones iniciales) pero no suficiente (hay sistemas muy sensibles que no son caóticos).
Entremos en materia metiendo el pie en el agua con un ejemplo muy simple: un sistema cuyo estado viene definido por una sola variable, x
x
, y una ecuación que determina cómo va evolucionando x
x
a lo largo del tiempo. Esa ecuación debe decirnos el valor de la variable en el paso n+1
n+1
a partir del valor en el paso anterior, n
n
. Supongamos que nuestro sistema viene definido por esta ecuación de evolución:
xn+1=xn2
xn+1=xn2
Simple, ¿no? Para saber el valor de x
x
en un paso, tomamos el del paso anterior y lo elevamos al cuadrado. Por ejemplo, empezando con x0=1
x0=1
, tenemos que x1=12=1
x1=12=1
, x2=12=1
x2=12=1
, etc. Claro, como x
x
cambia elevándose al cuadrado, si empezamos con 1 siempre tendremos 1. El valor de x
x
nunca jamás cambiará. Se trata de un caso particularmente simple de un sistema de por sí muy sencillo.
Pero si x0=1,01
x0=1,01
, tan sólo una centésima más, entonces la cosa sí cambia, pues 1,012 no es 1,01 sino 1,0201. Así, x1=1,0201
x1=1,0201
, x2=1,02012=1,0406401
x2=1,02012=1,0406401
, etc. Por ejemplo, en este caso, x100=7,316...
x100=7,316...
. Ah, pero si cambiamos una centésima hacia abajo, x0=0,99
x0=0,99
, entonces x1=0,9801
x1=0,9801
, y cada x
x
vale menos que la anterior, de modo que x100=0,133...
x100=0,133...
De hecho, llevémoslo al extremo: tras un número infinitamente grande de pasos, si x0=1,01
x0=1,01
, x tenderá a infinito, porque un número mayor que 1 al cuadrado es siempre mayor que sí mismo, mientras que si x0=0,99
x0=0,99
pasará lo contrario y el valor de x tenderá a cero. Si llamamos al valor de x
x
tras un número infinito de pasos estado final, estado final de nuestro sistema es infinito en un caso y cero en el otro, variando unas meras dos centésimas. ¡Pero lo mismo hubiera pasado si fueran dos millonésimas! x0=1,000001
x0=1,000001
y x0=0,999999
x0=0,999999
también divergen hacia los mismos valores. ¿Es o no es sensible a los valores iniciales? Ya lo creo que sí.
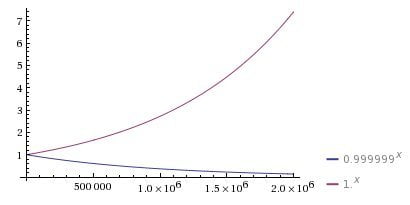
Gráficas de 1,000001x y 0,999999x generadas con la siguiente instrucción de wolframalpha.
¡Pero esto no es un sistema caótico! Si sólo hubiese este efecto, el caos sería una estupidez como un piano de cola. Sin embargo, espero que este primer ejemplo de un sistema definido por una variable y una ecuación nos sirva de trampolín para entender otro menos simple que sí es caótico. Aquí seguiremos el ejemplo de Robert May y nos dedicaremos a estudiar poblaciones… pero claro, no la de animales tan anodinos como los que estudiaba el australiano.
Conozcamos a…
Zweldreord es un planeta idílico y pastoral: prácticamente todo está cubierto de suaves colinas cubiertas de hierba verde y jugosa, con voraces arbolillos carnívoros de agradable olor y afiladas espinas que la fauna local bien sabe evitar, pero que han costado más de un disgusto a los ecólogos de la Galaxia. Cada año zweldreordano dura unos veinte años terrestres, con lo que sus estaciones son muy largas.
Y de entre todas sus criaturas ninguna es tan famosa como sus conejos.
El conejo zweldreordano es una criatura pequeña y adorable, con un pelaje suave y sedoso de color blanco como la nieve. A pesar de su pequeño tamaño, se trata de un animal de enorme voracidad, ya que es capaz de comer casi su propio peso en hierba en un día. Pero ni una cosa ni la otra es lo que los hace realmente especiales.
Estos conejos se reproducen a un ritmo fijo, que depende únicamente de un factor: la temperatura ambiente. En invierno, las conejillos zweldreordanos no tienen demasiado interés en el sexo opuesto; no dejan de reproducirse, pero lo hacen a un ritmo muy lento. En el verano, en cambio, se entregan a un frenesí reproductivo casi comparable al de los lutrinos.

Esto hace que la población de conejos zweldreordanos cambie muy bruscamente según pasa el año, y la evolución de estas poblaciones ha fascinado a los ecólogos durante siglos desde que Irneh Eracniop empezase a realizar observaciones sobre ellos, antes de su desafortunado incidente con un árbol local. “Algo que huele tan bien no puedeeAAAARRGGHH” fueron sus últimas palabras, registradas por su alumna de postgrado y heroína de nuestra historia, Florencia Elleursnetka, una Lemurina de Magallanes de gran perspicacia, enormes ojos y gran amor por los conejillos zweldreordanos.
Tras la muerte de su mentor, incapaz de obtener ninguna beca para seguir estudiando a los conejos, Florencia terminó trabajando para un ranchero sin escrúpulos de Zweldreord, Robento Maldibento. Maldibento era un Bovinoide, una especie muy parecida a las vacas lecheras terrestres oriunda de Betelgeuse. Los Bovinoides betelgeusianos tienen una horrible fama en la Galaxia, pues no son demasiado inteligentes, tampoco demasiado limpios y su ruindad es notoria – como ves, sólo se parecen a nuestras amables vacas en apariencia física.
El caso es que Robento se había enriquecido con negocios nada limpios en Betelgeuse, y al oír hablar de los conejillos zweldreordanos, su sedoso pelaje y su sensibilidad reproductiva a la temperatura, decidió iniciar un negocio de peletería en Zweldreord. Antes de entrar en producción, el malvado ungulado estableció un rancho de pruebas en Zweldreord con el que estudiar cómo obtener la máxima cantidad de conejos en el menor tiempo posible y del modo más barato.
De modo que Maldibento contrató a la pobre Florencia Elleursnetka, desesperada por obtener financiación para sus investigaciones con los conejillos, y le proporcionó una población de conejos y unas magníficas instalaciones con las que estudiar su reproducción. Para no depender de las estaciones zwelderordanas, la estación disponía de termostatos que permitían simular cualquier estación del planeta y “engañar” así al sentido reproductivo de los conejos.
Florencia se dedicó durante los siguientes meses a tratar de obtener una ecuación que predijese el número de conejillos que habría dependiendo de distintos factores; su motivación era, naturalmente, la simple curiosidad científica, y su ingenuidad le había impedido comprender la razón del interés de Maldibento en la población de conejos.
Afortunadamente para Florencia, se trataba de un sistema cuyo estado venía definido por una sola variable, x
x
, el número de conejos. Así, debía haber una ecuación que predijese xn+1
xn+1
a partir de xn
xn
. ¿De qué factores dependería esa ecuación?
Antes de nada, la estación disponía de una cantidad de hierba diaria que podía alimentar como mucho a un número determinado de conejos: la población nunca podría exceder ese número. Naturalmente, el objetivo de Maldibento era alcanzar un número de conejillos tan cercano a ese máximo como fuese posible, ya que estaría obteniendo el máximo beneficio para la inversión correspondiente en comida.
Por lo tanto, Florencia decidió utilizar x
x
para representar, no el número absoluto de conejos, que eran varios miles, sino la fracción de conejos sobre el máximo posible en la estación, es decir, el tanto por ciento sobre el máximo posible: x=0,5
x=0,5
, por ejemplo, significaría que hay la mitad de conejos que puede soportar la estación. x=1
x=1
significaría que la población está al tope, x=0,1
x=0,1
sería el 10% del máximo y x=0
x=0
significaría que los conejitos se han extinguido y Florencia está en un terrible aprieto.
El primer factor de la ecuación, creo, es evidente: el número de conejitos que nacen por cada conejo. La lemurina representó este factor con la letra r
r
; por ejemplo, r=1
r=1
significaba que nacía un gazapo por cada conejo de la generación anterior (dos por pareja), con lo que se mantenía el número neto. En el invierno zweldreordano, por ejemplo, nacía un conejillo de cada pareja, es decir, uno por cada dos conejos, r=0,5
r=0,5
, lo cual disminuía la población muy rápido durante esa estación del año.
El segundo factor también me parece muy claro: el número de conejos. Si r=2
r=2
, por ejemplo, cada generación duplica el número de la anterior. Pero no es lo mismo duplicar un número inicial de x=0,01
x=0,01
que duplicar un x=0,45
x=0,45
. Como r
r
es el número de gazapillos por conejo, al multiplicarlo por el número de conejos tendremos el número de conejitos total que nace en una generación determinada. Así, si $x3 = 0,2y
y
r = 2,porejemplo,tendremosqueenlasiguientegeneraciónhay
,porejemplo,tendremosqueenlasiguientegeneraciónhay
x4 = 0,4$.
Con esto, Florencia elaboró una versión simple de la ecuación del sistema. Si no consideramos ningún factor más –que los hay, pero paciencia–, la ecuación sería sencillamente:
xn+1=r⋅xn
xn+1=r⋅xn
Y esta ecuación, por cierto, no es de comportamiento caótico ni mucho menos. Esta ecuación no tiene en cuenta algo crucial: el hecho de que hay un máximo posible de conejos en la estación, puesto que la comida disponible es limitada. Pueden nacer cientos de millones de gazapos, pero si no hay comida para todos, algunos (o incluso muchos) morirán y no podrán reproducirse a su vez.
¿Cuántos conejitos sobrevivirán tras el nacimiento? Si hay mucha comida disponible, lo harán casi todos, pero si el número de conejos se acerca al máximo, la competencia por la comida será tremenda y muchos morirán. Por lo tanto, aquí tenemos algo en cierto sentido contrario al factor del nacimiento: cuantos más conejos hay, más gazapos nacen (lo cual es bueno para que la población aumente), pero menor porcentaje de ellos sobreviven (lo cual es malo).
Florencia representó este “factor sustento” de una manera bastante simple y que funcionaba muy bien. Supuso que el porcentaje de conejitos que sobrevivían era proporcional al porcentaje que “faltaba” para rellenar la población máxima. Por ejemplo, si hay x=0,5
x=0,5
, entonces el 50% de los conejitos sobrevirirán –ya que queda “la mitad de la comida disponible sin comer”, mientras que si x=0,9
x=0,9
, entonces sólo el 10% sobrevivirán, porque el 90% de la comida disponible ya está siendo devorada. Dicho de otro modo, el porcentaje de supervivientes es proporcional a (1−x)
(1−x)
.
Con la introducción de este factor final, Florencia obtuvo la ecuación que en la Tierra llamamos mapa logístico (y que fue, por cierto, la que utilizó Robert May en su estudio original):
xn+1=r⋅xn⋅(1−xn)
xn+1=r⋅xn⋅(1−xn)
Una vez lista, presentó sus resultados a Maldibento, que examinó la ecuación con ojos vacunos mientras se lamía la nariz.

“Interesante… interesante”, afirmó, sin entender ni media variable de la ecuación. “¿Con cuántos conejos cuenta la estación?”
“Con unos mil”, respondió Florencia.
“¿Y con cuántos contará en un mes, dado el coste de comida diario?”
“Bien, eso depende de la temperatura, que determina el ritmo reproductivo, claro… ahora mismo los termostatos determinan un factor de reproducción r=0,5
r=0,5
, lo que significa que la retroalimentación del sistema…“
“¡No me aburra con detalles!”, interrrumpió el Bovinoide con un mugido. “¡Dígame cuántas pie… quiero decir, cuántos conejitos tendré, con esta inversión, dentro de un mes!”
Pensemos con Florencia, pues.
Supongamos que empezamos con x0=0,5
x0=0,5
, el 50% del máximo de conejos. Cuando haya pasado una generación quedarán tan sólo x1=0,5⋅0,5⋅0,5=0,125
x1=0,5⋅0,5⋅0,5=0,125
. La siguiente generación sólo tendrá x2=0,5⋅0,125⋅0,875=0,0546875
x2=0,5⋅0,125⋅0,875=0,0546875
, etc. Pero lo mejor es que vayas viendo lo que sucede tú mismo; para ello hemos creado una página con algo de javascript que te permite modificar esos valores y ver la gráfica resultante: https://eltamiz.com/files/conejos.html, gracias a la ayuda de Unai, que hizo una parecida cuando hablamos de la secuencia de Fibonacci.
Te recomiendo que abras una pestaña nueva con la gráfica de los conejos para que puedas ir haciendo las modificaciones que te indique: aunque pondré algunos pantallazos a lo largo del texto, no puedo ponerlos de todos los pasos que haremos, con lo que tendrás que ir mirando lo que pasa tú mismo para “experimentar” el nacimiento del caos. Además, mis pantallazos son simples imágenes, pero en las gráficas producidas con el javascript puedes mover el ratón por encima de la gráfica y te mostrará el valor de la generación n
n
y los conejos x
x
en ese punto (gracias a Google, que en esto se sale).
Empecemos con el caso que acabamos de decir: introduce los valores de x
x
inicial 0,5 (un 50% de los conejos máximos), r=0,5
r=0,5
(cada generación nacen un 50% de los conejos de la generación anterior, es decir, una catástrofe ecológica), y n=10
n=10
(diez generaciones, porque no hace falta más para ver el destino de las criaturas). Verás algo como esto:
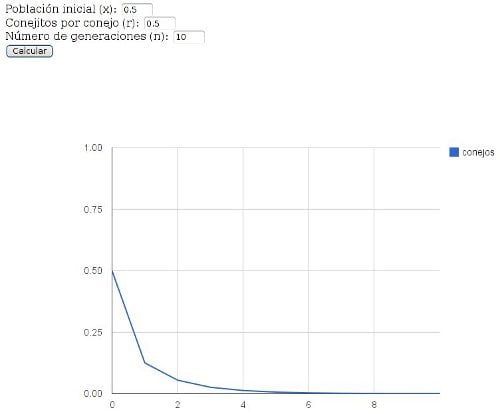
Como decía antes, en la pestaña del javascript puedes mover el ratón sobre la gráfica generada y ver el número exacto de conejos en cada generación. En este caso, puedes ver que tenemos un sistema muy predecible. Para comprobarlo, modifica ligeramente las condiciones iniciales: en vez de tener 0,5 de conejos en la generación inicial, cámbialo por cualquier valor entre 0 y 1 y verás que los pobres conejos están condenados, y este sistema no tiene la menor sensibilidad a las condiciones iniciales: x
x
tiende a 0 muy rápidamente independientemente del número inicial de conejos.
De modo que, tras un par de días con los termostatos en r=0,5
r=0,5
y tras algunos cálculos, Florencia volvió al despacho de Maldibento para explicar sus conclusiones.
“Con la temperatura actual, dentro de un mes no habrá conejos: la predicción es una extinción total.”Y, efectivamente, cuando el Bovinoide miró por la ventana de la jaula conejil, observó que quedaban muchos menos conejos de los mil que habían empezado el experimento.
“¿Una extinción total?”, exclamó Maldibento. “¡Aumente la temperatura entonces!”
“Desde luego, señor”, dijo la lemurina, deseosa de salvar a los conejillos. Y fue aumentando la temperatura de los termostatos poco a poco del 0,5 inicial hasta r=1
r=1
. Te recomiendo que pruebes, partiendo del mismo número de conejillos iniciales, a aumentar r
r
desde 0,5 poco a poco hasta 1, y verás lo que sucede.
Podríamos pensar que con ese factor tenemos una población de conejos estable, ya que cada conejo de una generación produce un conejo en la siguiente… pero claro, eso supone que no se muere ninguno una vez nacido –nuestro factor (1−x)
(1−x)
–, lo cual no es cierto. Cuando lo hayas ejecutado habrás visto, como la horrorizada Florencia, que con r=1
r=1
los conejos también se extinguen independientemente del número inicial que hubiese.
Es posible que con r=1
r=1
y n=10
n=10
no veas claro que los conejos se extinguen; si a lo largo del artículo te pasa algo así, recuerda que puedes modificar el número de generaciones para ir más allá en el tiempo. Si introduces, por ejemplo, n=500
n=500
, verás claramente el destino, lento pero inevitable, de los conejitos con r=1
r=1
. Una vez más, un sistema muy predecible y nada sensible a las condiciones iniciales, como puedes comprobar si varías el x
x
inicial.
Ahora bien, el valor r=1
r=1
representa el límite de un cambio cualitativo en el destino de los conejos; si pruebas con r = 1,01, por ejemplo, verás que los conejos ya no están condenados, sino que la población se estabiliza en un valor fijo muy pequeño, lo mismo que para cualquier otro valor de r entre 1 y 2, por ejemplo, r = 1,2:
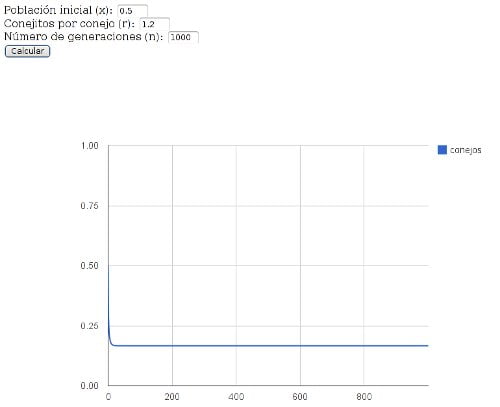
Esto alegró enormemente a Florencia, que vio que los conejos iban a salvarse. Su simplísima ecuación seguía prediciendo un estado final fijo, pero ahora ese estado final ya no era la extinción sino una cantidad estable de conejos; un estado final que no depende en absoluto de las condiciones iniciales. Prueba a cambiar x
x
por valores bastante extremos, como 0,01 o 0,99, y verás que en poco tiempo la población tiende a exactamente el mismo valor que antes (los ejes pueden cambiar de escala, pero si mueves el ratón sobre la gráfica verás que el valor siempre es igual).
Aunque interesante, sigue tratándose de un sistema muy simple. Puedes ir aumentando r
r
poco a poco para ver cómo la población se vuelve más “saludable” y tiende a un valor más alto, como sucedió según Florencia aumentaba la temperatura de la estación. Por ejemplo, en el caso anterior de r=1,2
r=1,2
, la población siempre termina siendo x=1/6
x=1/6
independientemente de cuántos conejillos haya al principio. Observa que, por ahora, te estoy mostrando un sistema nada caótico – más bien exactamente lo contrario.
Una vez obtenidos estos resultados, y con la población de conejilos estabilizada, la lemurina volvió una vez más al despacho de Maldibento con las buenas noticias.
“Hecho, señor”, anunció. “La población sigue las predicciones de mi modelo y se estabilizará en pocas generaciones.”
“¿Cuántos conejos entonces?”, preguntó su jefe tras tragar la bola de rumen que estaba masticando.
“Con la temperatura actual, un 16% del máximo posible, independientemente del número inicial”, respondió Florencia muy satisfecha.
“¿¡Un 16%?! ¿Está usted bromeando?”, bramó el futuro ranchero. “¡Necesito más, muuuUUUUuuucho más!”
“Sí, pero…“
“¡Aumente la temperatura! ¡Aumente la temperatura ahora mismo!”, ordenó el Bovinoide.
Y Florencia fue aumentando la temperatura de los termostatos hasta que la estación entera estaba ya bastante caliente y los trabajadores tuvieron que ponerse en ropa veraniega para soportarla. Los conejillos, sin embargo, fueron ganando vivacidad según subían los grados, y mostrando un lascivo interés los unos en los otros. Las nuevas generaciones se fueron nutriendo más y más.
Florencia observó, como harás tú mismo si lo pruebas, que el límite r=2
r=2
supone otro cambio cualitativo: a partir de ahí los conejos se reproducen de modo que hay más del doble de conejos nacidos por cada conejo de la generación anterior, y la cosa se vuelve un poco “loca”, pero no mucho. Verás que la población sigue, una vez más, tendiendo a un valor fijo, pero se alcanza más tarde y, hasta que se alcanza la estabilidad, la población sufre oscilaciones arriba y abajo, por ejemplo, con x=0,8
x=0,8
y r=2,8
r=2,8
para n=30
n=30
generaciones:
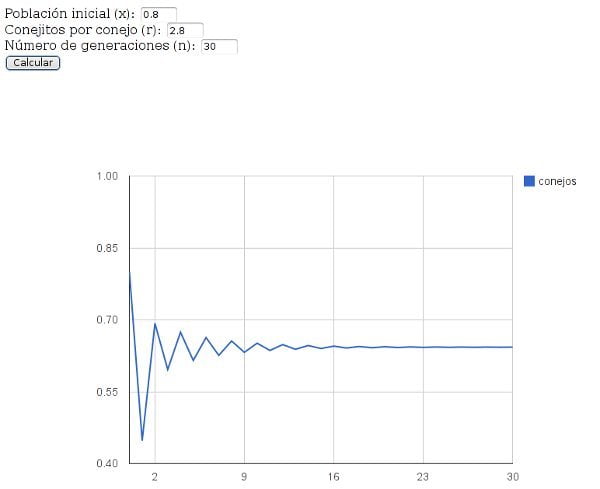
Ahora bien, si pensamos a largo plazo, la cosa realmente no ha cambiado nada, como puedes ver si en vez de mirar n=30
n=30
generaciones lo haces con n=1000
n=1000
generaciones. Al principio el sistema oscila, pero sigue siendo perfectamente predecible y (como verás si cambias el valor inicial de x) no nota en absoluto los cambios en las condiciones iniciales a largo plazo. Seguimos lejos del caos. Florencia sabía exactamente cómo iba a terminar la población de conejos.
Como ves, de lo que no depende el estado final, es decir, el número de conejos la cabo de infinidad de generaciones, es del número inicial de conejos: de lo que sí depende es de r
r
. De modo que podemos representar en otra gráfica –que ahora te puede parecer una tontería pero luego te ayudará mucho a comprender esto– el valor de “x final” dependiendo de r
r
. Como hemos visto, según aumenta r
r
aumenta el número final de conejos de manera bastante leve. La gráfica empieza en r=2,4
r=2,4
(porque para r
r
pequeños, como hemos visto, no pasan muchas cosas interesantes), y como ves, el valor de x
x
final aumenta según lo hace r
r
:
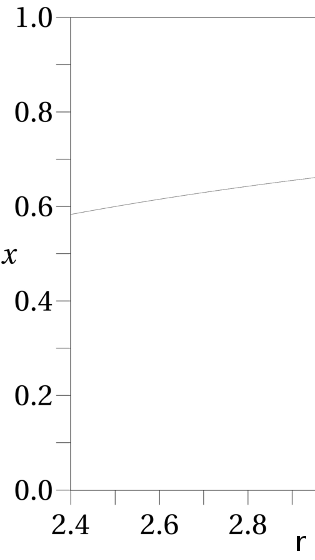
Cuando Maldibento vio esta gráfica, sonrió su sonrisa bovina y agitó las orejas con aprobación. No era muy avispado, pero sí lo suficiente como para entender que esa línea ascendente significaba, para su futura empresa peletera, muy buenas noticias.
“Bien… muuUUUUuuuy bien”, felicitó a su ingenua empleada. Al mirar por la ventana del vivero de conejillos se dio cuenta de que, efectivamente, el número se había estabilizado en un valor del 65% y los conejillos mostraban una actitud muy provechosa para él (y placentera para ellos). “Aumente la temperatura un poco más”, ordenó.
“Sí, pero debe usted saber que…“, trató de decir Florencia una vez más.
“Aumente. La. ¡TEMPERATURA!”, retumbó la voz del enorme toro en el despacho. Y Florencia obedeció, aunque con ciertas dudas.
Pero llegamos, por fin, a un punto en el que las cosas se vuelven bastante interesantes y, en mi opinión, deliciosas, aunque supusieran una sorpresa para Florencia. A partir de r=3
r=3
se produce otro cambio cualitativo – la población ya no se estabiliza en un valor único. Esto no significa que el sistema se vuelva impredecible; como verás cuando pruebes con un valor de r
r
ligeramente superior a 3, lo que sucede es que ahora la población de conejos oscila entre dos valores fijos que no dependen de la población inicial en absoluto. Es como si se hubiera producido una “bifurcación” de la población final de conejos en dos valores oscilantes que sólo dependen de r
r
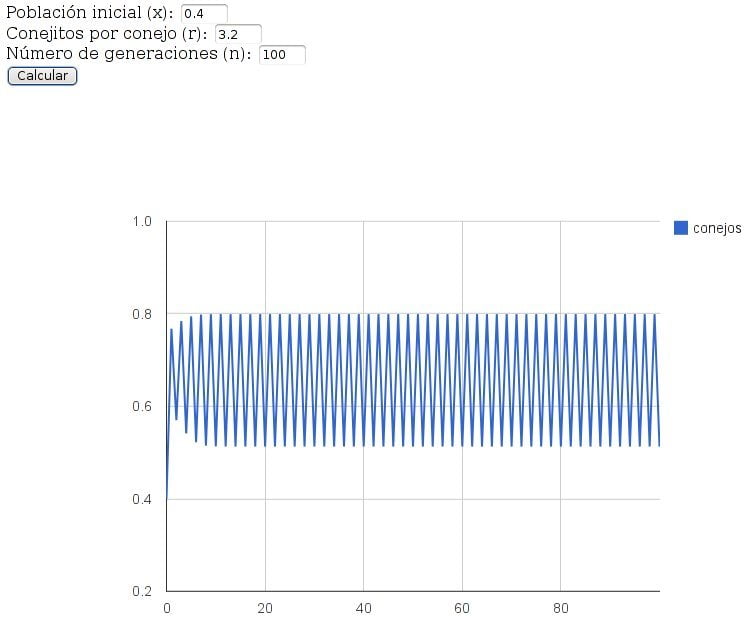
. Observa el caso x=0,4
x=0,4
, r=3,2
r=3,2
y n=100
n=100
:
Una vez más, si cambias el valor inicial de x
x
verás que los dos valores de oscilación no dependen de él. Según aumenta r
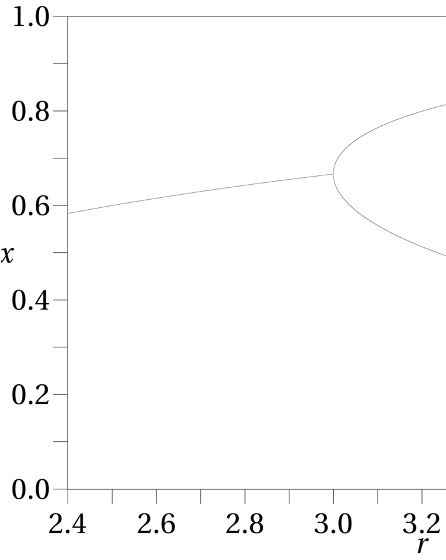
r
, eso sí, los dos valores oscilantes se van alejando ligeramente el uno del otro, como puedes ver si aumentamos algo nuestro diagrama anterior del valor final de x
x
dependiendo de r
r
. Claro, ahora no hay un único valor final, sino dos, con lo que es como si el tronco de un árbol se hubiera bifurcado; lo que ves, por cierto, se llama mapa de bifurcación del sistema por razones obvias:
De modo que, según aumentaba la temperatura de los termostatos, Florencia se encontró con una sorpresa: en vez de tener una población de conejos cada vez más próxima al máximo según nacían más conejitos de cada pareja, la población empezó a oscilar arriba y abajo de manera regular. Una generación había muy pocos conejitos, pero como nacían bastantes y había mucha comida, sobrevivían casi todos, con lo que la siguiente generación era muy numerosa. Pero claro, entonces nacían muchos conejitos y apenas había comida, con lo que la población disminuía mucho. Era como un reloj de péndulo de enorme precisión: tic, tac, tic, tac, entre dos valores fijos.
Naturalmente, su jefe no estaba tan satisfecho como ella con esto, ya que nó tenía la menor curiosidad sobre el comportamiento de los conejillos. Un valor oscilante no era tan fácil de vender a futuros inversores de sus granjas peleteras como un valor fijo. Sin embargo, en su obtusa mente bovina, Maldibento encontró una solución muy simple a este problema:
“Aumente la temperatura”, ordenó a la lemurina cuando ésta le mostró los resultados de arriba.
“Antes de hacerlo, debe usted saber que mi mentor Irneh Eracniop descubrió un efecto secundario de la temperatura, que…“
“¡MuuUUUUUUUUuuu!”
“Sí, sí, aumento la temperatura…“, se rindió la pobre lemurina.
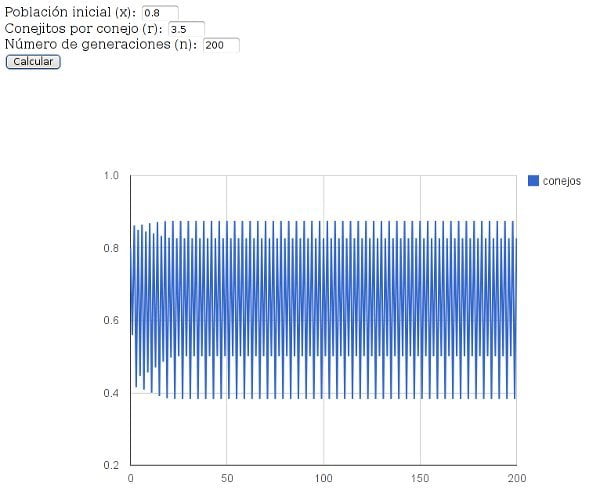
En pocos días, al aumentar aún más la temperatura y con ella el ritmo reproductivo de los conejitos, a partir de r=3,45
r=3,45
se produjo una segunda “bifurcación”: cada valor anterior se convierte en dos valores oscilantes, con lo que ahora la población oscila entre cuatro valores. Aquí tienes el ejemplo que puedes ver tú mismo con x=0.8
x=0.8
, r=3,5
r=3,5
y 4n=200
4n=200
:
Una vez más –y disculpa si soy repetitivo–, aunque el comportamiento sea curioso, sigue siendo perfectamente ordenado: la población oscila entre cuatro valores fijos que no dependen de las condiciones iniciales. La población sigue un ciclo de cuatro pasos – un número muy grande de conejos, con lo que no hay comida y muchos mueren en la siguiente generación; un número muy pequeño tras la extinción, luego hay suficiente comida para crecer, pero no muchos conejos, con lo que el crecimiento es relativo; un número grande tras el paso anterior, demasiado grande para estar en equilibrio, con lo que hay una nueva extinción pero no tan brutal como la primera, y finalmente, dado el estado óptimo de la población (suficientes conejos para crecer, no demasiados de modo que no hay déficit de comida) un gran crecimiento que de vuelve la población al número grande inicial… y así una y otra vez. Como un reloj que hace tic, toc, clac, tac, tic, toc, clac, tac…
El mapa de bifurcación muestra los cuatro estados finales:
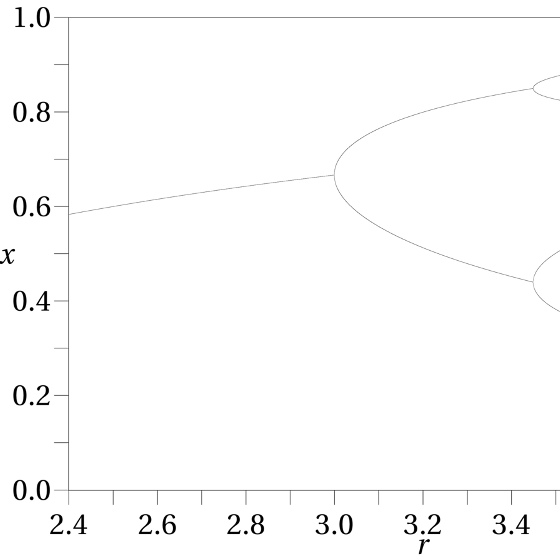
Esta vez, sudando como un pollo, la pobre Florencia ni siquiera enseñó sus resultados a su jefe. “¡Aumente la temperatura, aumente la temperatura!”, se dijo a sí misma con sorna. Y siguió aumentando la temperatura aún más, contra su buen criterio y contra las advertencias del insigne Irneh Eracniop.
Pero de los caóticos sucesos que acaecieron entonces a Florencia, Maldibento y los conejillos zweldreordanos hablaremos la semana que viene en la conclusión de este artículo: no es bueno dañar demasiado las neuronas de una sentada. ¡Hasta entonces!
Créditos: Pedro Gómez-Esteban González. (2009). El Tamiz. Recuperado de: https://eltamiz.com/


