

Tras la pausa de rigor para permitir que vuestras erosionadas mentes se recuperen, hoy volvemos con una nueva entrega de la delirante serie sobre los Alienígenas matemáticos. En el último artículo de la serie conocimos a los lascivos y adorables lutrinos y dañamos nuestro tejido neuronal enfrentándonos con la Paradoja de Ross-Littlewood, una de las muchas que tienen que ver con el concepto de infinito. Hoy, para cambiar de tercio, volveremos a una paradoja probabilística, más al estilo de la de Monty Hall.
Antes de que sigas leyendo, un aviso: no lo hagas. Este artículo, como todos los de la serie, es ridículamente pedante, absurdo, no llega a ninguna conclusión útil, está plagado de bromas insulsas y humor negro, muerte y seres abyectos. Leerlo supone una experiencia casi tan desagradable como escribirlo, y hace honor al lema oficial de la serie, dicho lisa y llanamente: la lectura de este texto es ortogonal a cualquier uso práctico del período temporal que requiere. Avisado estás.
Dicho esto, hoy nos zambulliremos en una paradoja planteada por primera vez, hasta donde he podido saber, por el inimitable Martin Gardner en 1959 en la revista Scientific American. En su forma original, como la paradoja de los dos niños, hablaba de parejas que tenían hijos que podían ser niños o niñas, y luego ha resurgido de muchas otras maneras, todas ellas igualmente anodinas e inapropiadas para nosotros. Aquí la plantearemos, como siempre en esta serie, de modo que involucre apuestas de vida y muerte, tentáculos y sensaciones horripilantes. ¿Preparado?
Si eres un lector habitual de la serie, conoces la conquista de la Tierra por los horrendos Alienígenas matemáticos, y los espantosos experimentos de estos monstruos galácticos con los seres humanos en general y, por supuesto, contigo en particular: imagina, estimado y sagaz lector, que tras la conquista del planeta has sido capturado por las babosas criaturas, y te encuentras en una celda lóbrega y oscura en la que hay tres de los Alienígenas matemáticos sonriéndote (¿puede haber algo más truculento?).
El más grande y terrorífico de los monstruos se dirige a ti con voz áspera y te dice:
“Bienvenida a este experimento, criatura. Has sido elegido al azar entre nuestros prisioneros para darte una oportunidad de ser libre”. El resto de los alienígenas emiten un sonido gorgoteante que no puedes interpretar de otra forma que como risa. Un extraño olor a amoníaco inunda la habitación. “Por si te sirve de consuelo, xuglurz”, susurra el monstruo mientras rezuma babas, “éste es un experimento en el que, hasta ahora, al menos la mitad de tus congéneres han salido con vida y libres. El resto…“ El monstruo no continúa la frase, pero varios de sus estómagos gurgutan placenteramente.
“Te presento a mis dos ayudantes hoy, Lorwelarclis y Rinntemardrag”, sibila tu anfitrión mientras señala a sus dos acompañantes con un apéndice tentaculado primero y otro después. Los seres te sonríen cuando el mayor pronuncia sus nombres, revelando múltiples hileras de dientes puntiagudos. Observas que frente a cada uno de los dos hay una mesa con cuatro vasos de color negro, tapados.
El alienígena asiente, complacido. “Veo que ya has observado los vasos frente a mis ayudantes: son la clave de este experimento. Dos de los cuatro vasos frente a Lorwelarclis contienen sustancias repugnantes que vosotros, humanos, consideráis agradables: zumo de naranja en uno y zumo de limón en otro. Los otros dos vasos, sin embargo, contienen compuestos deliciosos que, para vosotros, son mortales: cianuro en uno y estricnina en el otro. Naturalmente, los vasos son opacos y están tapados, para que sea imposible determinar el contenido de cada vaso salvo dando un trago.”
A continuación, el monstruo señala hacia el otro alienígena con un tentáculo. “Los cuatro vasos frente a Rinntemardrag contienen las mismas cuatro sustancias: zumo de naranja, zumo de limón, cianuro y estricnina.” Observas que, una vez más, los cuatro recipientes son negros y están tapados como los de Lorwelarclis.
“Tanto Rinntemardrag como Lorwelarclis conocen el contenido de cada vaso, por supuesto”, continúa el baboso ser, estremeciéndose de placer ante tu evidente desazón. “Pero, naturalmente, no van a decirte cuáles contienen veneno y cuáles el repugnante zumo de frutas terrestres. Ahora, deja que te cuente cuáles son las reglas del… bueno, supongo que podríamos llamarlo ‘juego’“. La reluciente piel del alienígena se estremece con una pequeña y gorgoteante risita.
“Como tal vez hayas adivinado ya, patético ser”, dice el tirano espacial, “para salir de aquí debes beber el contenido de uno de los ocho vasos. Una vez que lo hayas hecho, serás libre de salir por esa puerta…. ¡si es que no has tenido la mala suerte de elegir uno de los vasos con veneno, por supuesto!”. Al decir esto, los tres Alienígenas matemáticos estallan en carcajadas espantosas, rociándote con espumarajos de baba ácida de la cabeza a los pies. Tras un buen rato, las criaturas acaban calmándose y tu tenebroso anfitrión continúa la explicación.
“Naturalmente, el experimento no consiste sólo en esto… la probabilidad de salir con vida es evidente, la elección es inane y no hay el menor interés en ello. Como te he dicho antes, xuglurz, más de la mitad de tus congéneres han salido con vida de la habitación en este experimento, y la elección aleatoria de un vaso sólo te proporcionaría un 50% de probabilidad de supervivencia. Mi magnanimidad” –ante esa palabra, los otros dos alienígenas ríen socarronamente– “es muy grande.”
“Para empezar, elige dos vasos de cada mesa”, ordena el baboso ser. De manera que haces lo que te dice y, puesto que no hay nada que pueda ayudarte en la decisión, escoges dos vasos al azar de los cuatro frente a Rinntemardrag y otros dos de los que tiene Lorwelarclis. Los dos ayudantes retiran los vasos que has descartado, y se quedan con los dos elegidos en cada mesa.
“Ahora, como muestra de mi benevolencia, voy a permitirte que hagas una pregunta a Lorwelarclis y otra a Rinntemardrag sobre el contenido de los vasos que has elegido”, anuncia el monstruoso ser, agitándose con excitación. “Pero no cualquier pregunta: a uno de los dos puedes preguntarle si algún vaso frente a él contiene zumo, y al otro puedes preguntarle si algún vaso frente a él contiene una bebida en concreto de las cuatro posibles.”
A pesar de que se trata de una orden extraña, no tienes mucho que opinar, de manera que sigues las instrucciones. Puesto que nada distingue a Lorwelarclis de Rinntemardrag, lo haces al azar, y en primer lugar preguntas a Lorwelarclis si frente a él hay zumo. La criatura asiente, agitando los tentáculos nerviosamente y frunciendo todos los ceños, decepcionado porque no has tenido la mala suerte de elegir los dos vasos con veneno de los cuatro que había frente a él.
A continuación, preguntas a Rinntemardrag si uno de los dos vasos frente a él contiene zumo de naranja. El monstruo te lanza una mirada hambrienta y huraña, contrariado, y luego lanza un “Sí, xuglurz” a regañadientes, por razones similares a las de Lorwelarclis: si consigues escapar, la cena de los monstruos será mucho menos jugosa e interesante.
Y, por fin, llega la temida e inevitable orden del Alienígena que lidera el crudelísimo experimento:
“Bien, especimen”, anuncia el monstruo, todos y cada uno de sus ojos amarillentos, vidriosos y supurantes clavados en ti con hambre asesina, “elige uno de los cuatro vasos y bebe de él, y entonces podrás irte libre.”
De modo que, en este momento de la macabra narración, hagamos la pausa de rigor para que pienses durante un rato sobre la situación. Sabes que frente a Lorwelarclis hay al menos un vaso de zumo, y que frente a Rinntemardrag hay un vaso de zumo de naranja. Debes beber uno de los cuatro vasos frente a ti: o bien uno de los dos que tiene Lorwelarclis, o bien uno de los dos que tiene Rinntemardrag. Si tu vida dependiera de ello, ¿cuál elegirías, si es que hay alguna diferencia? Piénsalo un momento, con papel y lápiz si es necesario, antes de seguir leyendo.
La respuesta más habitual a esta pregunta es que da igual. El razonamiento suele ser algo así: “En ambos casos tengo asegurado un zumo, es decir, al menos un 50% de probabilidad de salvarme. Si el otro vaso también es zumo, me salvo seguro, y si es veneno, me salvo un 50% de las veces para ambos Alienígenas.” Muy intuitivo, muy sencillo… e incorrecto. De ahí la paradoja: sí que importa cuál de los dos eliges.
La respuesta correcta es que, sin dudarlo, debes beber de uno de los vasos de Rinntemardrag. Hacerlo maximiza tus posibilidades de salvarte, aunque esto no sea evidente a primera vista; si me hiciste caso y has usado papel y lápiz, es más probable que hayas encontrado la solución correcta. Pero vayamos por partes.
En principio, cuando eliges dos de los cuatro vasos de cada alienígena, existen seis posibles resultados, todos igualmente probables: zumo de naranja y zumo de limón, zumo de naranja y estricnina, zumo de naranja y cianuro, zumo de limón y estricnina, zumo de limón y cianuro y, finalmente, estricnina y cianuro. De manera que, antes de que hayas hecho ninguna pregunta, podríamos mirar el problema como esta tabla de posibilidades, en la que hemos representado los dos zumos con sus colores naturales, el cianuro en verde y la estricnina en morado (los colores dan igual, claro, es sólo para llevar la cuenta), con una calavera en cada veneno:
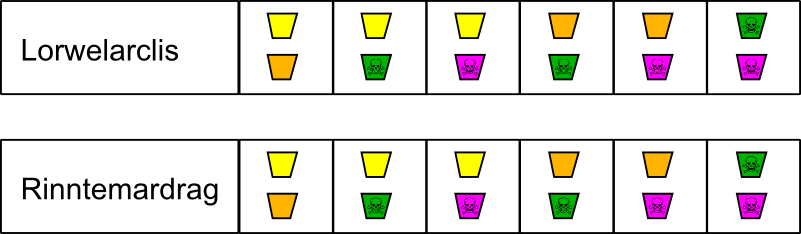
Pero, una vez que haces las preguntas, sabes que algunas de esas opciones no son posibles. En el caso de Lorwelarclis, al menos un vaso es de zumo, de manera que –para gran alivio tuyo– puedes descartar el caso de los dos venenos. En el caso de Rinntemardrag la restricción es más fuerte: puesto que tiene delante zumo de naranja, puedes descartar todos los casos que no contienen esa bebida. Tachando las opciones imposibles, tenemos las siguientes para cada uno:
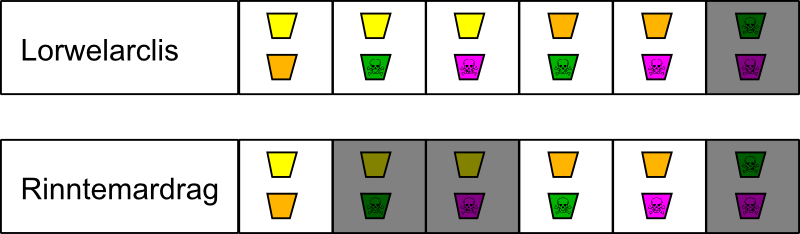
¿Ves la clave de la cuestión? Tras la información adicional al hacer la pregunta a cada uno, ambas opciones han cambiado, pero no de la misma manera. Para los dos casos hemos eliminado algunas opciones que ahora son imposibles pero, dado que la pregunta hecha a Rinntemardrag era más específica, en su caso hemos eliminado más opciones.
Esto puede parecer poco importante, pero es esencial por una razón: en ambos casos mantenemos una posibilidad común muy importante y alentadora, la de que se trate de los dos vasos de zumo y no haya veneno. En ambos casos eliminamos la peor opción, la de que ambos vasos sean de veneno. Pero, al eliminar más opciones, en el caso de Rinntemardrag estamos haciendo que la probabilidad del caso óptimo (dos vasos de zumo) sea mayor. Veamos qué sucedería, tras la pregunta, si elegimos beber de uno de los vasos de Lorwelarclis o de uno de los de Rinntemardrag.
Si bebemos de Lorwelarclis, estaremos en una de las cinco posibles opciones del dibujo de arriba (la sexta no es posible tras conocer el hecho de que tiene zumo delante). De esas cinco opciones, en una nos salvamos seguro (ambos vasos tienen zumo), y en cualquiera de las otras cuatro hay un vaso de zumo y otro de veneno y, puesto que bebemos de uno de los dos vasos al azar, moriremos la mitad de las veces y nos salvaremos la otra mitad. En total, las posibilidades de salvarnos son de 1/5 · 100% (un quinto de las veces bebemos zumo seguro) + 4/5 · 50% (cuatro quintos de las veces tenemos un 50% de probabilidad de salvarnos), es decir, un 60% de probabilidades de salvarnos, definitivamente una mejora desde el 50% que hubiéramos tenido si el magnánimo Alienígena anfitrión no nos hubiera permitido preguntar nada.
Si bebemos de Rinntemardrag, estaremos en una de las tres posibles opciones del dibujo de abajo (las otras tres no son posibles tras conocer el hecho de que tiene delante zumo de naranja). De esas tres opciones, una vez más, hay una excelente en la que nos salvamos seguro (ambos vasos con zumo), y en cualquiera de las otras dos hay un vaso de zumo y otro de veneno, lo que nos confiere un 50% de probabilidad de supervivencia si bebemos de uno de los dos vasos. Por lo tanto, la probabilidad de sobrevivir si bebemos de Rinntemardrag es de 1/3 · 100% (un tercio de las veces bebemos zumo seguro) + 2/3 · 50% (dos tercios de las veces tenemos un 50% de probabilidad de beber zumo y salvarnos), es decir, un 66,67% de probabilidades de salvarnos.
De modo que la elección que deberías haber hecho, pues te otorga un 6,7% más de probabilidades de salvarte, es la de beber de Rinntemardrag. Pero sigamos con nuestra historia.
Tras realizar unos cuantos cálculos mentales y asegurarte de que todo encaja, te diriges decidido hasta la mesa de Rinntemardrag y coges uno de los dos vasos al azar, dándole un trago con decisión. Empiezas a caminar hacia la puerta pero, de pronto, empiezas a encontrarte muy, muy mal.
“Has elegido bien, xuglurz, y elogio tu acumen matemático”, susurra el Alienígena mayor casi con dulzura. “Desgraciadamente, un 33,33% de probabilidad sigue siendo apreciable, y el zumo de naranja que Rinntemardrag tenía delante… era el otro.”
Al menos…, piensas según la habitación empieza a dar vueltas y las criaturas empiezan a cambiar de color en oleadas lascivas e iridiscentes, al menos, he maximizado la prob… Y todo es oscuridad.
__________
Créditos: Pedro Gómez-Esteban González. (2009). El Tamiz. Recuperado de: https://eltamiz.com/


